报告人：初保志（Rutgers University-New Brunswick）

时 间：2023年6月1日11:00

地 点：海韵园实验楼105报告厅

内容摘要:

For dimension n ≥ 3, there is a classic result due to Liouville:

∆u = 0, u > 0, R ⁿ ⇒ u ≡ constant.

There is also a renowned Liouville-type theorem for Yamabe equation due to Caffarelli-Gidas-Spruck (under additional conditions, by Obata and Gidas-Ni-Nirenberg):

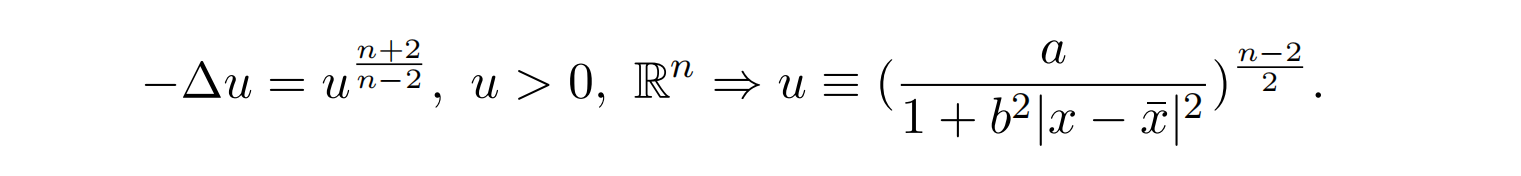
In a joint work with Yanyan Li and Zongyuan Li, we generalize both Liouville-type theorems above along the direction of conformal invariance to the fully nonlinear version. And our both generalized theorems are necessary and sufficient statements by realizing the same borderline. We expect they will be useful in treating scalar curvature changing-sign problems in conformal geometry. If time permits, I will also discuss some applications of our Liouville Theorems, including local gradient estimates, Harnack inequalities, etc.

个人简介：

初保志，2019年本科毕业于亚搏ag捕鱼app，现博士就读于Rutgers University-New Brunswick, 师从李岩岩教授。

联系人：夏超